You're using it wrong!

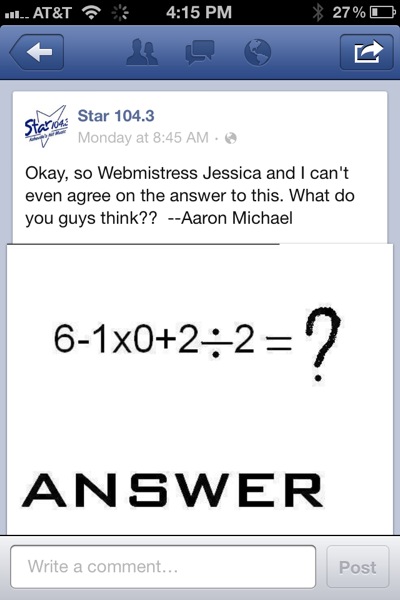
​This problem, and ones like it, have become popular on Facebook.  People enjoy arguing about "the right way" to do these problems.  The discussions revolve around PEMDAS, or the mathematical order of operations.

While I would never want to deprive anyone of some good ol' math fun, these problems frustrate me.  The answer to the question is:  Use some parentheses please!  No one writes strings of arithmetic like this.  They use parentheses to make their meaning clear.​

People find these problems fun, at least in part, because 6th grade math books teach problems like these.  But this is an exercise in missing the point.  What is the point, you ask?  Let me tell you!​

The point of PEMDAS (parentheses, exponents, multiplication, division, addition and subtraction.  Or, Please Excuse My Dear Aunt Sally!) is to allow us to write algebraic expressions without parentheses!  A simple quadratic like 3x^2 + 5x - 6 would require three sets of parentheses without order of operations.

My son's recent school work actually finished strong.  ​The obligatory word problem at the bottom of the worksheet went like something like this:

Write an expression for buying x shirts for $10 each and y hats for $5 each.

So the answer, 10x + 5y is actually a great example of when and why we want to multiply before we add.​  Three cheers for context!  Boo and hiss for random strings of arithmetic!

PS:  The correctly written problem would read:​

6 - (1*0) +(2/2) = 6 - 0 + 1 = 7​

engagement

I've spent a lot of time thinking about improving student engagement.  It seems that many of the solutions are simple.  Here's one that worked well last week.​

A student asks for help on a homework problem.  You all know the drill.  You do the problem on the board.  Five people pay attention.  You figure that if one person asked, probably the whole class should be following along.  But most aren't.  ​

I simply decided to take their lack of interest off the table.  I asked the whole class to read the problem.  Then I randomly picked a student to start the problem.​

[sidebar:  I have been highlighting my seating chart.  Every time someone participates, whether voluntarily or by my choice, I highlight their name on my seating chart.  When everyone has a yellow highlight, I switch to green.  It gets a bit messy and in time it looks like it's filled with psychedelic asterisks.  It allows me to call choose carefully who I call on, while ensuring that no one can be ignored.]​

We scaffold through the problem with about 8 different students being called on to contribute to the solution.  The entire class is engaged and everyone has seen a correct solution.​

Now as to why most of class doesn't care about a solution to a challenging homework problem.  Well, if I had all the answers, the comments would be closed.​

procedures

This is probably more of rant than an enlightening observation, but...​

What's up with these rules we teach our kids about moving decimal points around for multiplication and division?  First off, these procedures are rarely used by anyone.  We use a calculator for goodness sake.  But more importantly, these rules become pure magic.  There is no number sense, no common sense and no math sense.  My son has no clue how many times $0.25 should go into $6.  There is no checking for the reasonableness of an answer.  There is just a procedure and a box around the answer.  One of his "word problems" (read: do the same thing you just did 12 times and put a word at the end of your answer) had four-digits divided into five-digits.  The answer was clearly a bit less than 10.  ​But he had no clue which way to divide, much less about where his answer might be.  I used a calculator to verify that the answer was 9 and saved him some pain.

I hope the common core will solve things like this.  I don't claim to know all the answers.  But there's got to be a better way.​

NOTE:  I'm quite impressed with my son's teacher.  I'm sure she is forced by California's calculator-free assessments to teach much of what she does.​

In the zone

I've spent some time this summer reading Colvin's Talent is Overrated.  I have read a lot of it.  But am trying to figure out more about how to apply its principles to my teaching life.  Specifically, I want to delibrately practice my teaching craft in such a way that I am improving.

But I realized that the book's principle of delibirate practice cuts two ways for a teacher:  we need to think about how we practice, but we also need to think about how our students practice.  

I had two students come after school for tutoring in AP Stats a lot this last year.  They both earned a 2 (not passing) on the AP test.  Heart-breaking 2's.  Every AP teacher knows what this feels like.  Hard working students who you like and they don't quite make it.

But it makes me wonder how I had them practice.  It was probably too routine.  Too familiar.  Learn the basics.  "Here, do another one" (just like the one you just did).  

I could be too hard on myself.  Maybe without the tutoring they would have earned 1's.

But the idea that ignites my imagination is the Learning Zone.  Colvin talks about the comfort zone, learning zone and panic zone.  Students usually come to tutoring because they feel panicked.  But do I let them slide all the way to comfort?  Or do I keep them learning?

For that matter, how do I keep my class in the Learning Zone?  I've been trying to lecture less and let students work more.  But Hunter's "Guided practice" may not be learning.  At least not enough learning.  It may just be comfortable practice that looks a lot like the lecture.

Much to learn!

Just stop

If we're talking about technology in a math classroom.  You know, calculators, computers, Wolfram Alpha, all that cool stuff.  And you say "Well if your calculator runs out of batteries..."  or "If you don't have an internet connection..." or something in that vein.  Then I would consider our conversation to be over.  And I would safely say that you're not thinking very carefully about the issues surrounding technology and learning.

It might be that you just need more time.  And that you haven't thought carefully enough yet.  Or you live in California and you've given in to the demands of the CST's.

But I can't believe that you've really thought carefully about your own life and how you do math.  Or watched someone under the age of 25 and how they interact with technology.  

More on what careful thinking on these topics looks like later...

I like...

I've worked with a few long term substitute teachers recently.  They have both commented at the end of the day "I like working with the AP classes!"  The problem is, the students didn't seem to share their enthusiasm.

I don't say this to be mean.  I say this because it made me pause as I looked in the mirror.  I have classes I like to teach (AP Stats!).  And my students seem to like taking the class with me.  But all that is really beside the point.  The essential question is simple, yet forgotten--Do they learn in my class?  

It's about the learning.  Period.

It's not about me liking them or me liking them.  It's not about having fun.  It's about students learning to think.  Don't get me wrong, I don't think animosity makes for a learning state of mind.  But at the end of the day, I hope my students learn.  

Ignite

I did a 5 minute Ignite talk for Key Curriculum Press at the CMC Palm Springs conference.  Here's the link.

Homework

I stopped grading homework this year.  It isn't worth anything.  Not "points", not a percent.  I also noticed that I was assigning less and less.  I have a mixed feelings about this.  Reading Dan Myer about this made me feel better.  I wonder if he still feels the same as he did four years ago.

Not giving out points for papers filled with work of dubious value was definitely a good decision.  I don't think I'll ever go back.  Now how much to assign and how to maximize class time.  That's still the battle.

Deadhorse #1

It's hard to let things go.  But if we're ever going to teach deeper and better, we've got teach fewer topics.  So here's the beginning of a list:

Rationalizing the denominator.  Time to kill it.  Call it dead.  

A bit of history:  this topic only exists because armed with a square root table and a piece of paper, it is easier to scratch out root-2 divided by 2 than 1 divided by root-2.  In other words, this topic has the same shelf life as interpolating on log tables. (Which I learned.  Despite the TI SR-52 sitting on my desk.)

You say some nice things about this topic.  You can connect it to other ideas.  But it doesn't have a point and its time to kill it.